12 Jan 2019 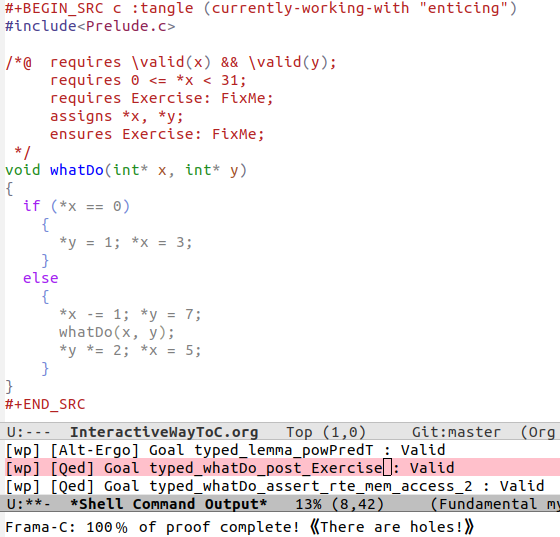
Abstract

Do you know what the above program accomplishes? If you do, did you also spot a special edge case?
We aim to present an approach to program proving in C using a minimal Emacs setup so that one may produce literate C programs and be able to prove them correct –or execute them– using a single button press; moreover the output is again in Emacs.
The goal is to learn program proving using the Frama-C tool –without necessarily invoking its gui– by loading the source of this file into Emacs then editing, executing, & proving as you read along. One provides for the formal specification of properties of C programs –e.g., using ACSL– which can then be verified for the implementations using tools that interpret such annotation –e.g., Frama-C invoked from within our Emacs setup.
Read on, and perhaps you'll figure out how to solve the missing FixMe pieces 😉
The intent is for rapid editing and checking. Indeed, the Frama-c gui does not permit editing in the gui, so one must switch between their text editor and the gui. Org mode beginning at the basics is a brief tutorial that covers a lot of Org and, from the get-go, covers “the absolute minimum you need to know about Emacs!”
If anything, this effort can be construed as a gateway into interactive theorem proving such as with Isabelle, Coq, or Agda.
The article aims to be self-contained –not even assuming familiarity with any C!
The presentation and examples are largely inspired by
- Gilles Dowek's exquisite text Principles of Programming Languages.
- It is tremendously accessible!
- Allan Blanchard's excellent tutorial Introduction to C Program Proof using Frama-C and its WP Plugin.
Another excellent and succinct tutorial is Virgile Prevosto's ACSL Mini-Tutorial. In contrast, the tutorial ACSL By Example aims to provide a variety of algorithms rendered in ACSL.
There are no solutions since it's too easy to give up and look at the solutions that're nearby. Moreover, I intend to use some of the exercises for a class I'm teaching ;-)
1 Introduction
Despite its age, C is a widely used language and so is available on many platforms. Moreover, many systems rely on code historically written in C that needs to be maintained.
The traditional way to obtain confidence that a program correctly works is to provide inputs we believe to be representative of the actual use of the program and verify the results we get are correct. Incidentally, the unexpected cases are often not considered whereas they are generally the most dangerous ones. Since we cannot test everything, we need to employ great care in selecting good tests.
Since it is hard to answer “Is our software tested enough?”, we consider mathematically proving that there cannot be problems at runtime. That is, a specification of the expected behaviour is provided, which is satisfied by the resulting program –note the order: Specify then obtain code! This two-stage process can produce errors in either stage, yet whereas testing ensures “the program avoids the bugs we tested against” this approach is a big step ensuring “the program doesn't contain bugs that don't exist in the specification.”
The goal here is to use a tool to learn the basics of C program proof –Frama-C: FRAmework for Modular Analysis of C code. In particular, to demonstrate the ability to write programs without any error by emphasising the simple notions needed to write programs more confidently.
Testing is ‘dynamic analysis’ since it requires the actual execution of programs, whereas our program proof approach is ‘static’ since no execution is performed but instead we reason on a semantic model of the reachable states. The semantics associated with the C language control structures and statements we will use is known as Hoare Logic. One writes a “Hoare Triple” {G} S {R} to express that “Starting in a given state (satisfying) G, the execution of S terminates such that the resulting state (satisfies) R”.
How does one prove such a triple? Programs are constructed from a variety of pieces, so it suffices to look at each of those. That is, {G} S {R} has the code S transform the required predicate R to the given G –since we usually know what is required and it is the goal of the program. In general, we find the weakest precondition that works since then it allows the largest possible number of inputs; if G is at least as strong as the weakest precondition, then our program is correct but may allow less then the largest amount of possible inputs.
For example, {5 ≤ x ≤ 10} x ≔ x + 1 { 3 ≤ x ≤ 11} is a correct program that ends in state 3 ≤ x ≤ 11, however its precondition could be weakened to 2 ≤ x ≤ 10 thereby allowing many more valid inputs.
In Frama-C, we do not use curly braces like this for such assertions but instead express our properties as code annotations using the ANSI C Specification Language –ACSL or “axel”. The weakest precondition plugin uses the annotation and the code to automatically ensure the program is correct according to the Hoare Logic fashion mentioned earlier.
1.1 Getting Started
The aim of this section is to introduce the Emacs controls that bring C to life within literate code.
| Key Press | Elisp Command | Description |
Enter <s then TAB |
─ | Produces a “Hello World” C template program. |
F6 |
(interpret) |
Execute currently focused code blocks in a new buffer. |
F7 |
(show-code) |
Shows currently focused code blocks in a new buffer. |
F8 |
(frama-c) |
Open the Frama-C gui on the currently focused code blocks. |
F9 |
(frama-c-no-gui) |
Invoke Frama-C on the currently focused code blocks in a new buffer. |
Which code blocks are currently under focus is controlled by the command
(currently-working-with "nameHere"), which produces a file nameHere.c that is used
for the utility functions. If multiple blocks use the same filename, then the file is
appended to.
While reading this tutorial, bring/take code blocks in/out of focus by
toggling between (currently-working-with "nameHere") and
(not-currently-working-with "nameHere") —that is, simply prepend not-.
Remember to undo such a toggle when you're done with a code block.
When no name is provided to [not-]currently-working-with, the name of the buffer is used.
1.1.1 Exercise: Hello World
- Insert the text
<sthen press theTABkey. - A new C program template has appeared.
- Press
F6to execute the code in another buffer. - Press
F7to inspect the code in another buffer. - Alter the program to output your name, press
F6.
Now toggle that code block so that you are not currently working with it.
- Make a change to the code block, such as printing 42. Notice that
F6refers to the old file on disk since there is no currently focused block.
1.1.2 Exercise: Verifying Swap
Consider the fully annotated swap algorithm, i.e., remove the not- prefix,
// #include<stdio.h> // for IO /*@ requires \valid(a) && \valid(b); assigns *a, *b; ensures *a == \old(*b); ensures *b == \old(*a); */ void swap(int* a, int* b) { int tmp = *a; *a = *b; *b = tmp; } int main() { // printf("Hello World!\n"); int a = 42; int b = 37; //@ assert Before_Swap: a == 442 && b == 37; swap(&a, &b); //@ assert After_Swap: a == 37 && b == 42; return 0; }
We can see that Frama-C proves these assertions by obtaining “green bullets” beside them if we execute
frama-c-gui -wp -rte myfile.c
Or check-boxes beside them if we instead execute
frama-c-gui -gui-theme colorblind -wp -rte myfile.c
The best way to know which options are available is to use
frama-c -wp-help
We will however use the special Emacs calls defined at the bottom of this file,
frama-c and frama-c-no-gui, to avoid having to switch between a terminal and a
text editor. Thank-you extensible editor Emacs ⌣̈ ♥
- Press
F8to invoke the Frama-C gui. - Press
F9to invoke Frama-C within Emacs and obtain status about the program proof.
If you uncomment the IO matter, Frama-C may yield an error. Separate your IO into its own driver file! Invoke Frama-C only on programs you want to prove –without any IO.
Go back to the above example, and change the first assertion in main,
~a == 42, to assert that a equals 432. Now invoke M-x framac-no-gui, or press F9,
to obtain the message,
Frama-C: 90﹪ of proof complete!
Moreover, another buffer will be open and in red will be highlighted,
[wp] [Alt-Ergo] Goal typed_main_assert_Before_Swap : Unknown (Qed:0.63ms) (57ms)
This indicates that, in method main, the named assertion Before_Swap could not be proven.
Now revert all alterations and in the specification of swap, alter
ensures *a ==== \old(*b); to become ensures *a == \old(*a);, thereby expressing
that the value of a is unaltered by the program. Checking this yields a false
assertion! Neato.
As such, I suggest the following literate process:
- Write your code in Org-mode code blocks,
- Check it works with
frama-c-no-gui(F9) orframa-c(F8).- If we open the gui, we may right-click on a function name and select
Prove function annotations by WPto have our assertions checked. - Remember that the frama-c gui does not allow source code edition.
- If we open the gui, we may right-click on a function name and select
- Investigate output, then make changes in source file and re-check.
Observe
- Program proof is a way to ensure that our programs only have correct behaviours, described by our specification;
- It is still our work to ensure that this specification is correct.
1.2 A Prelude
Since C's #include is essentially a copy-paste, we can re-export other libraries
from a make-shift ‘Prelude’.
// Artefacts so that exercises let the system progress as much as possible. // //@ predicate Exercise = \false; //@ predicate FixMe = \false; #define FixMeCode // Tendency to require this header file to specfiy avoidance of overflow. // #include<limits.h>
We will continue to be (currently-working-with "Prelude") in the future to add more
content. For now, we put the artefacts needed to let the exercises pass.
The use of
\falseis not the most appropriate, since its occurrence in a precondition vacuously makes everything true! This is something that should change.The current setup produces only
.cfiles, whence we use the prelude by declaring#include "Prelude.c".Forgive my use of a.cfile in-place of a header file. The alternative is to force all code block names to end in a.c.
2 Basic Constructs
Recall that a Hoare Triple {G} S {R} expresses that if execution of program S is begun
in a state satisfying proposition G then it terminates in a state satisfying proposition R.
We usually know R –it is the required behaviour on S after all– but otherwise we usually
only have a vague idea of what G could possible be.
Dijkstra's weakest precondition operator ‘wp’ tells us how to compute G from R
–in the process we usually discover S.
Hence, all in all, programming begins with the required goal from which code is then derived.
Details
Post-conditions R are expressed using the ensures clause, and dually pre-conditions G
are expressed using requires clauses. These G are properties assumed for the input
and it is the callers responsibility to ensure that they are true
–recall that when a contract is breached, the implementation may behave arbitrarily.
Since ‘wp’ is intended to compute the weakest precondition establishing a given
postcondition R for a statement S, it necessarily satisfies
{ G } S { R } ≡ G ⇒ wp S R
The left side may be rendered using ACSL,
// @ assert G; S; // @ assert R;
The WP plugin for Frama-C essentially works by computing wp S R then attempts to obtain
a proof for G ⇒ wp S R.
In particular, by the reflexivity of implication, ‘wp’ guarantees to produce a
precondition so that the following Hoare triple is valid.
{ wp S R } S { R }
Most programming languages have, among others, five constructs:
Assignment, variable declaration, sequence, test, and loop.
These constructs from the imperative core of the language.
Since programs are built using such primitive control structures, it suffices to define
wp “by induction” on the shape of S.
One reasonable property we impose on wp from the outset is:
If S establishes R which implies R′, then S also establishes R′.
Monotonicity: R ⇒ R′ implies wp S R ⇒ wp S R′
That is, {wp S R} S {R′}
Whence for each definitional clause of wp, we must ensure this desirable property is held.
Details
Imperative programs alter state, as such a statement S is essentially a function
that transforms the memory state of the computer.
Expressing in English what happens when a statement is executed is possible
for simple examples, but such explanations quickly become complicated and imprecise.
Therefore, one introduces a theoretical framework reifying statements as state transformers.
The two popular notions are the “forwards” ⟦S⟧ moves current state to a new state,
whereas we are working with “backwards” wp S which takes a desired state and yields
a necessary previous state. The forward notion ‘executes’ a program by starting in
the empty state and stepping through each command to result in some final state.
Whereas the backwards notion takes an end goal and suggests which programming constructs
are needed to obtain it.
Hence, ‘forwards’ is verification whereas ‘backwards’ is correct-by-construction
programming.
Suppose there is an infinite set Var of variables and an infinite set Val of values,
which are integers, booleans, etc. In the ‘forwards’ notion, a state is a partial
function from variables to values –`partial' since it may be undefined at some
variables, since we usually use only finitely many
in our programs anyways. E.g., state {x ↦ 5, y ↦ 6} associates the value 5 to variable x
but is undefined for variable z. Dually, in the ‘backwards’ notion, a state is a predicate of the
variables and their values that satisfy the predicate; e.g., the previous example state
corresponds to the predicate x = 5 ∧ y = 6, where z can have any value.
Hence the predicate formulation is more relaxed and we shall refer to it instead.
2.1 Assignment
The assignment construct allows the creation of a statement with a variable
x and an expression E. The assignment statement is written x = E;.
- Variables are identifiers which are written with one or more letters.
- Expressions are composed of variables, constants, and operator calls.
- Sometimes one notates assignment by
x ≔ Eeven though it is invalid C code.
To understand the execution of an assignment, suppose that within the
recesses of your computer's memory, there is a compartment labelled x.
Obtain the value of E –possibly having to look up values of variables
that E mentions– then erase the contents of x and fill the compartment
with the newly obtained value.
The whole of the contents of the computer's memory is called a state. We also say “predicate R is the current state” as shorthand for: The current state is (non-deterministically) any variable-value assignment such that predicate R is true.
All in all, executing x ≔ E loads memory location x with the value of expression E;
hence state R is satisfied after an assignment precisely when it is satisfied
with variable x replaced by expression E. For example, wp (x ≔ x+1) (x = 5) ≡ (x+1 = 5).
wp (x ≔ E) R ≡ R[x ≔ E]
Before being able to assign values to a variable x, it must be declared,
which associates the name x to a location in the computer's memory.
Variable declaration is a construct that allows the creation of a statement
composed of a variable, an expression, and a statement. This is written
{T x = e; p}, then variable x can be used in statement p, which is called
the scope of variable x.
( When p has no assignments, functional programmers would call this statement
a let statement since it lets x take on the value e in p. )
Details
- Division:
If both arguments are integers, then the operation rounds down; write, e.g.,
5 / 2.0to mark the result as floating point. - Modulo: The number
a % bisa - b * (a / b). - Ternary Conditional: For all types, the expression
(c) ? t : fyieldstif booleancholds and isfotherwise. - A useful inclusion: 2*109 <= 232 <= 2*1010
2.1.1 Overshadowing & Explicit Scope Delimitation
Imperative languages generally do not allow the declaration of the same variable multiple
times, e.g., the following program crashes with error: redefinition of ‘x’.
#include<stdio.h> // for IO int main() { int x = 3; printf("x has value: %d", x); int x = 4; printf("x has value: %d", x); return 0; }
However, if we explicitly delimit the scope of a variable by using braces, then we can obtain multiple declarations:
#include<stdio.h> // for IO int main() { int x = 3; printf(" x has value: %d", x); // 3 { int x = 4; printf("\n x has value: %d", x); // 4 } return 0; }
When explicitly delimiting scope, it is the most recent declarations that are used. We say that earlier declarations are hidden, or overshadowed, by the later declarations.
Details
int main() { int x = 3; //@ assert x == 3; { // Begun new scope // Old facts are still true. //@ assert x == 3; // Now overshadowing ‘x’ int x = 4; // This new ‘x’ is equal to 4. //@ assert x == 4; } // Back to the parent scope. // In this scope, ‘x’ still has its orignal value. //@ assert x == 3; return 0; }
2.1.2 Constant Variables
Constant variables are variables which may have only one initial value that
can never be changed. A non-constant variable is called mutable, which is
the default in imperative languages. For example, the following
crashes with error: assignment of read-only variable ‘x’.
#include<stdio.h> // for IO int main() { const int x = 3; x = 4; printf("x has value: %d", x); return 0; }
2.2 Sequence
A sequence is a construct that allows a single statement to be created out of
two statements p and q; it is written {p q}.
The sequence is executed in state s by first executing p in state s thereby
producing a new state s' in which statement q is then executed.
- The statement
{p₁ {p₂ { ... pₙ } ...}}can also be written{p₁ p₂ ... pₙ}.
Usually a ‘;’ symbol is used in favour of a space, with braces, to yield,
wp (S₁;S₂) R ≡ wp S₁ (wp S₂ R)
The pre-condition of the second statement becomes the post-condition of the first statement. Hence, we “push” along the post-condition into a sequence: In the upcoming swapping example, we read the proof steps from bottom to top!
Rendered pointfree, i.e., ignoring R, this rule becomes: wp (S₁;S₂) = wp S₁ ∘ wp S₂.
Recall that we need to ensure monotonicity is satisfied, and indeed: If R ⇒ R′, then
wp (S₁;S₂) R ≡ wp S₁ (wp S₂ R) -- Definition of wp on sequence ⇒ wp S₁ (wp S₂ R′) -- Monotoncity for Sᵢ, twice; with assumption R ⇒ R′ ≡ wp (S₁;S₂) R -- Definition of wp on sequence
Neato!
Moreover, notice we have the useful ‘transitivity’ property for Hoare triples:
{G} S₁ {R′} ∧ {R′} S₂ {R}
≡ (G ⇒ wp S₁ R′) ∧ (R′ ⇒ wp S₂ R) -- Characterisation of wp
⇒ (G ⇒ wp S₁ R′) ∧ (wp S₁ R′ ⇒ wp S₁ (wp S₂ R)) -- Monotonicity of wp
⇒ (G ⇒ wp S₁ (wp S₂ R)) -- Transitivity of implication
≡ G ⇒ wp (S₁;S₂) R -- Definition of wp on sequence
≡ {G} S₁;S₂ {R} -- Characterisation of wp
Exercise: Show that wp (x ≔ E; S) R ≡ (wp S R)[x ≔ E].
2.3 Skip
The “empty sequence” is denoted {} or just ; in the C language.
It is also commonly known as the skip construct and its importance is akin to that
of zero to addition.
wp skip R ≡ R
The “do nothing” program skip is rendered as simple ; or as whitespace in the C language.
This program does not alter the state at all, thus it truthifies R precisely when R
was true to begin with.
Most often this appears in a weakening/strengthening form,
...code here... //@ assert P; //@ assert Q; ...code here...
Where P ⇒ Q is provable.
More concretely,
/*@ requires 3 < a < 9; @ ensures -20 <= \result <= 99; */ int using_skip(int a) { //@ assert our_strong_pre: 3 < a < 9; //@ assert weakened_intermediary: -7 <= a <= 14; //@ assert weakening_futher: -20 <= a <= 99; return a; }
Woah! It looks like the identity function somehow transforms input satisfying
3 < x < 9 to input satisfying -20 ≤ x ≤ 99.
Wait, the former implies the latter and that's just the definition of wp on skip.
The above example suggests the following calculation,
(G′ ⇒ G) ∧ {G} S {R} ∧ (R ⇒ R′)
≡ (G′ ⇒ G) ∧ (G ⇒ wp S R) ∧ (R ⇒ R′) -- Characterisation of wp
⇒ (G′ ⇒ wp S R) ∧ (R ⇒ R′) -- Transitivity of implication
⇒ (G′ ⇒ wp S R) ∧ (wp S R ⇒ wp S R′) -- Monotonicity of wp
⇒ (G′ ⇒ wp S R′) -- Transitivity of implication
≡ {G′} S {R′} -- Characterisation of wp
That is, strengthening the precondition or weakening the post-condition leaves a Hoare triple valid. In some industry circles –e.g., C#–, this is referred to as contravariance (antitone) in the input and covariance (monotone) in the output.
For example, if G′, G, R, R′ were classes such that G′ is a subclass of G
and R is a subclass of R′, then the program S takes an input of type G yielding an
output of type R′. However, any input of type G′ can be cast into the parent-class
type G and, likewise, R objects can be cast into the parent-type R′.
Thus, program S can also take the type of G′ to R′.
Writing <: for ‘sub-type’, or ‘sub-class’, we have argued,
Provided G′ <: G and R <: R′
Then
G → R <: G′ → R′
It is now easier to see that the second argument of function-type former ‘→’ stays
on the same side of the <: symbol, whereas it is flipped for the first argument.
Completely unrelated –or not– a nearly identical property holds for implication: If G′ ⇒ G and R ⇒ R′ then (G ⇒ R) ⇒ (G′ ⇒ R′). How coincidental … or not! \\ ( Foreshadowing: Curry-Howard Correspondence! )
Anyhow, this strengthening-weakening law will be useful when computing the wp of a statement directly is difficult –and possibly unhelpful– but we have a stronger precondition and so it suffices to use that. ( Foreshadowing: Loops! )
Before we close, here is an exercise to the reader: An alternate proof of the above law.
(G′ ⇒ G) ∧ {G} S {R} ∧ (R ⇒ R′)
≡ {G′} skip {G} ∧ {G} S {R} ∧ {R} skip {R′} -- ???
⇒ {G′} skip; S {R} ∧ {R} skip {R′} -- ???
⇒ {G′} skip; S; skip {R′} -- ???
≡ {G′} S {R′} -- skip is no-op & can be removed.
The last hint in the above calculation deserves some attention.
- Rendered pointfree, i.e., ignoring R, the skip rule becomes: wp skip = id.
- Where id is the identity function: id(x) = x.
- “Program Equality”: Say
S ≈ Tprecisely whenwp S = wp T.- Two programs are considered equal precisely when they have the same observational behaviour –i.e., can satisfy the same set of post-conditions R.
- Identity of Sequence Theorem:
S ; skip ≈ S ≈ skip ; S. - Likewise, define wp abort R ≡ false – i.e.,
abortis a program that crashes on any input. - Zero of Sequence Theorem:
S ; abort ≈ abort ≈ abort ; S.
2.4 Examples Using the Assignment, Sequence, Skip Rules
To avoid having to write the verbose \at(x, Pre) to refer to the value of a variable x
before method execution, we may use a ghost variable: A variable whose purpose is only
to make the assertions provable, and otherwise is not an execution-relevant variable.
#include<limits.h> /*@ requires \valid(x) && \valid(y); @ requires INT_MIN < *x + *y < INT_MAX; @ requires \separated(x, y); // Exercise: It's a swap, why is this needed? @ assigns *x, *y; */ void swap(int *x, int *y) { //@ ghost int X = *x; //@ ghost int Y = *y; //@ assert *y == Y && *x == X; //@ assert *y == Y && (*x + *y) - *y == X; *x = *x + *y; //@ assert *y == Y && *x - *y == X; //@ assert *x - (*x - *y) == Y && *x - *y == X; *y = *x - *y; //@ assert *x - *y == Y && *y == X; *x = *x - *y; //@ assert *x == Y && *y == X; // 𝓢𝓽𝓪𝓻𝓽 upwards reading from here; // each assertion is obtained by the assigment, skip, and sequence rules. }
Here is a more complicated exercise that also makes use of external functions…
Details
#include "Prelude.c" #define RAND_MAX 32767 /*@ @ assigns \nothing; @ ensures 0 <= \result <= RAND_MAX; */ int rand(); /*@ requires min <= max; @ requires min + RAND_MAX < INT_MAX; @ requires max - min < INT_MAX; @ assigns \nothing; @ ensures min <= \result <= max; */ int random_between(int min, int max) { int it = rand(); //@ assert weakening: 0 <= it <= RAND_MAX; //@ assert assignment_rule_again: FixMe; it = it % (max - min + 1); // @ assert simplify: FixMe; // @ assert assignment_rule: FixMe; it = it + min; // @ assert min <= it; // Start at the bottom, and push assertion upwards! // The assertion names are also intended to be read upwards; // Each justifies how it was obtained. return it; // That is, // return (rand() % (max - min + 1)) + min; }
2.5 Test; Conditional
A test is a statement formed from a Boolean expression and two statements; it is
written \\ if (b) p else q –sometimes a ‘then’ keyword is used for readability, but
such is not valid C code.
This is executed in a state by evaluating the Boolean
then deciding which branch to execute in the same state.
wp (if B then S₁ else S₂) R ≣ if B then wp S₁ R else wp S₂ R
≡ (B ⇒ wp S₁ R) ∧ (¬ B ⇒ wp S₂ R)
A conditional ensures R precisely when its branches each ensure R.
Observe the following calculation,
{ G } if B then S₁ else S₂ { R }
≡ G ⇒ wp (if B then S₁ else S₂) R -- Characterisation of wp
≡ G ⇒ (B ⇒ wp S₁ R) ∧ (¬ B ⇒ wp S₂ R) -- Definition of wp on conditional
≡ (G ⇒ B ⇒ wp S₁ R) ∧ (G ⇒ ¬ B ⇒ wp S₂ R) -- Characterisation of meets
≡ (G ∧ B ⇒ wp S₁ R) ∧ (G ∧ ¬ B ⇒ wp S₂ R) -- Shunting
≡ {G ∧ B} S₁ {R} ∧ {G ∧ ¬ B} S₂ {R} -- Characterisation of wp
That is, Hoare triples on a conditional ‘distribute’ into the branches with each branch precondition obtaining the branch guard.
2.6 Loop
A loop is a construct formed from a Boolean expression and a statement; it is
written while (b) p.
A loop is one of the ways in which we can express an infinite object –which may
fail to terminate– using a finite expression. Indeed, its executional behaviour
can be understood by realising it as a shorthand for the expression
if (b) {p if (b) {p if (b) ...
else skip}
else skip}
else skip
Where skip is the fictional statement that performs no action when executed.
To understand the semantics of the loop:
- Let
giveup, terminatebe aliases forabortandskip. Recalling that a loop is a shorthand for an infinite nesting of conditionals, we try to approach it as a limit of finite approximations.
while (b) q ≈ limₙ pₙ Where: p₀ = if (b) giveup else terminate p₁ = if (b) {q ; if b giveup else terminate} else terminate ⋯ pₙ₊₁ = if (b) {q; pₙ} else terminate;- The statement
pₙtries to execute the statementwhile (b) qby completing a maximum ofntrips through the loop. If, afternloops, it has not terminated on its own, it gives up. If the loop terminates in m trips, it also terminates in n ≥ m trips.
- ∀ m. pₘ defined ⇒ ∀ n ≥ m. pₙ defined
- ∀ m. pₘ defined ⇒ ∀ n ≥ m. pₙ ≈ pₘ
Where ‘defined’ means it terminates without aborting.
- Hence, by these two claims, we know that the sequence pₙ either never defined or it is defined beyond a certain point, and in this case, it is constant over its domain.
- Hence:
while(b) q ≈ limₙ pₙ.
The definition of ‘wp’ for loops is complicated and generally unhelpful, however from it we can prove the so called “Invariance Theorem”: If a property is maintained by the body of the loop and there is an integral value expressed using the body's variables that starts out non-negative and is decreased by each loop pass, then the loop will terminate and the property it maintained will be true.
{Inv ∧ B ∧ bf = c} S {Inv ∧ bf < c}
⇒
{Inv ∧ bf ≥ 0} while(B) S {¬B ∧ Inv}
A property that is maintained to be true throughout the loop is referred to as an
invariant. In contrast, a value that changes through every pass
–such as the number of passes remaining, the bf– is known as a variant.
In Frama-C rendition,
/*@ loop invariant ⋯ // property that is maintained by the loop body @ loop assigns ⋯ // variables that are altered by the loop body @ loop variant ⋯ // a bound on the total number of loops */ while(B) S;
Incidentally the primary function of the assigns clause is that variables its does
not mention essentially have the invariant property of being equal to their value
before the loop. That is, the assigns clause reduces clutter regarding constants
from the invariant!
Details
#include<limits.h> /*@ requires N >= 0; @ requires N * (N + 1) /2 < INT_MAX; @ assigns \nothing; @ ensures \result == N * (N + 1) / 2; */ int euclid(int N) { int sum = 0; int n = 0; //@ assert invariant_intially_estabished: 2 * sum == 0 * (0 + 1); /*@ loop invariant main_item: sum == n * (n + 1) / 2; @ loop invariant always_in_range: 0 <= n <= N; @ loop invariant range_for_sum: 0 <= sum; // Exercise: Why can we comment out the following two lines? @ loop invariant no_overflow1: n < INT_MAX; @ loop invariant no_overflow2: sum <= INT_MAX; @ loop assigns n, sum; @ loop variant N - n; */ while(n != N) { //@ assert sum + n < INT_MAX; n = n + 1; //@ assert sum + n <= INT_MAX; sum = sum + n; //@ assert sum <= INT_MAX; } //@ assert invariant_and_not_guard: n == N && sum == n * (n + 1) / 2; //@ assert post_condition: sum == N * (N + 1) / 2; // rewrite_post: 2 * sum == N * (N + 1); // Not true, due to ‘rounding’! return sum; }
Exercise: Why is sum ≤ INT_MAX true at the end of the loop body? Fill in the proof:
sum ≤ INT_MAX ≡ n * (n + 1) / 2 ≤ INT_MAX -- ??? ⇐ n * (n + 1) / 2 ≤ N * (N + 1) / 2 ≤ INT_MAX -- Transtivitity of ≤ ≡ N * (N + 1) / 2 ≤ INT_MAX -- ??? ≡ true -- ???
Here's a simple exercise,
Details
#include<limits.h> /*@ requires a + 10 < INT_MAX; @ ensures \result == \old(a) + 10; */ int look_ma_no_new_locals(int a) { //@ ghost const int A = a; int i; // So we can refer to this ‘i’ *after* the loop. /* // @ loop assigns ???; // Fix me. @ loop invariant a == 666; // Fix me. @ loop invariant 0 <= i <= 10; @ loop variant 666; // Fix me. @*/ for(i = 0; i != 10; i++) a++; //@ assert after_loop_guarantees: i == 10 && a == A + i; //@ assert weakening_previous_gives: a == A + 10; return a; }
Warning Without the loop assigns, you are more likely to have trouble proving a loop
is correct!
Now a bit harder…
Details
#include<limits.h> /*@ assigns \nothing; @ ensures 0 <= \result <= 1; */ int random_bool(); // { return random_between(0, 1); } /*@ requires \valid(it); @ requires *it + max <= INT_MAX; // @ requires FixMe -- a property on `max`; // @ assigns FixMe; @ ensures \old(it) <= it <= it + max; */ void increment_randomly(int *it, int max) { /*@ loop assigns i, *it; @ loop invariant *it == \at(*it, Pre) + i; // @ loop invariant range_of_i: FixMe; // @ loop variant FixMe; */ for(int i = 0; i != max && random_bool(); i++) (*it)++; }
3 ACSL Properties
3.1 Predicates
Our invaraints were getting out of hand, the trouble can be mitigated by defining our own
predicates rather than just using the built in ones. However, such definitions must be
functional in nature: They do not produce side-effects, such as altering state.
Moreover, they are generally parameterised by a label that refers to the C memory state
in which they would be invoked –within the definition we cannot however reference the
special labels Here, Pre, Post. Otherwise parameter passing is by value as in C.
The predicate keyword declares Boolean values functions:
/*@ predicate name_here {Label₀, …, Labelₖ} (type₀ arg₀, …, typeₘ argₘ) =
@ // A Boolean valued relationship between all these things.
*/
// An integer memory location remains unaltered between given program points. // /*@ predicate unchanged{L0, L1} (int *i) = \at(*i, L0) == \at(*i, L1); */ int main() { int i = 13, j = 12; DoSomeWork: j = 32; //@ assert unchanged{DoSomeWork, Here}(&i); return 0; }
More usefully, there is the need to ensure a given integer is indeed a non-negative length of an array.
/*@ predicate valid_array(int* arr, integer len) = @ 0 <= len && \valid(arr + (0 .. len - 1)); */
Notice that we did not specify a memory label.
That's okay, one is provided for us and the entire definition is considered to transpire
at that memory location. In particular, unlike the previous example, we cannot refer to
distinct memory locations –after all we haven't named any!
At the call site, the implicit memory location would be Here thereby referring to the
current memory state –however we may still explicitly provide a different label at the
call site.
3.2 Logic Functions
Predicates must be either true or false, but logic functions are methods that
can be invoked in our specifications –you may have noticed that C methods cannot
be called in a specification, which is reasonably since they may produce side-effects!
Since assignment, sequence, and loops rely on side effects they now suddenly become
useless and our definitions must rely on recursion.
Such logical functions generally need not worry about runtime issues such as overflow
–which however must be handled at the call site, if need be.
/*@ logic return_type function_name {Label₀, …, Labelₖ} (type₀ arg₀, …, typeₘ argₘ) =
@ // A formula using the arguments argᵢ, possibly at labels Labelᵢ
*/
//@ logic integer factorial(integer n) = (n <= 0) ? 1 : n * factorial(n-1);
If we wrote a program that contained many occurrences to factorial then the definition
would need to be invoked each time. If the occurrences all happened, for example, on the
same input, say 12 –any larger would be an unsigned int overflow– then it might
make matters faster if we simply had that as a lemma that is proven once and used many
times by the underlying provers. Indeed this can be accomplished by using the lemma
phrase, and this can be done for any property.
//@ lemma name_of_property {Label₀, …, Label₀}: property_here ;
For example,
//@ lemma lt_plus_lt: \forall integer i,j; i < j ==> i + 1 < j + 1;
3.3 Axiomatic Definitions
Sometimes a proof may take too long to be proven, or it cannot be proven with the back-end provers, and, moreover, we do not wish to bother with its proof directly. In such cases, we may tell Frama-C to trust our judgement and take our word for it –if we're not careful, our ‘word’ may lead us to conclude false = true!
/*@ axiomatic my_axioms { @ axiom antisymmetry: \forall integer i, j; i <= j <= i ==> i == j; @ } */
Unlike lemmas, which require a proof, axioms are simply assumed to be true. It is the responsibility of the user to ensure no inconsistencies arise, as in:
//@ axiomatic UhOh{ axiom false_is_true: \false; } int main() { // Examples of proven properties //@ assert \false; //@ assert \forall integer x; x == 31; //@ assert \false == \true; return 0; }
However, axiomatic definitions of recursive functions are useful since the underlying
provers do not unroll the recursion when possible
–after all, we are simply declaring the type of a function and some properties about
it, which incidentally, happen to be its defining equations.
/*@ axiomatic Factorial { logic integer factorial(integer n); axiom factorial_base: \forall integer i; i <= 0 ==> factorial(i) == 0; axiom factorial_inductive: \forall integer i; i > 0 ==> factorial(i) == i * factorial(i - 1); } */
A small subtlety is that access to memory locations must be specified in the function headers, for example:
/*@ axiomatic is_constant { predicate constant{L}(int * a, integer b, integer e, integer val) reads a[b .. e-1]; axiom constant_empty{L}: \forall int * a, integer b, e, val; b >= e ==> constant{L}(a, b, e, val); axiom constant_non_empty{L}: \forall int * a, integer b, e, val; b < e ==> ( constant{L}(a,b,e, val) <==> constant{L}(a,b,e-1, val) && a[e-1] == val ); } */
4 Functions
We will be proving code blocks satisfy Hoare triples, but code blocks are essentially methods with the given predicate acting as a pre-condition and the required predicate acting as post-condition. As such, we investigate Hoare triples by using methods.
A contract stipulates under what conditions a method will behave
–if those conditions are not met, then it's behaviour may be arbitrary.
For example, a method may behave in a manner ensuring \\ x > 1/y under the condition y > 0,
and it may do anything it wants –such as aborting the system or setting x = -1–
when that condition is not met.
All in all, a function call establishes property R precisely when evaluating its arguments then executing the function body together establish the property.
wp ℱ(t₁, …, tₙ) R ≡ wp (x₁ ≔ t₁; ⋯ ; xₙ ≔ tₙ; ℬ) R where ℱ(x₁, …, xₙ) = ℬ -- Definition of ℱ
4.1 What are Functions?
Functions permit abstraction over program design since parts may be constructed independently and also promotes avoidance of repetition.
Unlike functional languages where the result of a function is the final
term in its body, imperative languages signal result values by the return keyword;
which immediately stops execution of the function regardless of the keyword's position.
Functions which return no value but instead perform some effectful action, i.e., are procedures,
are marked with the void keyword in-place of a return type –surprisingly, this ‘return type’
is not a type at all! One cannot declare a variable of type void.
Function calls that yield a value are terms whereas those that do not constitute statements.
Details
#include<stdio.h> // for IO int f(){ return 3;} void g(){ printf("g(): Hello There!"); } int main() { // Valid invocations int x = f(); f(); // Bad form! Result is discarded. g(); // T y = g(); // Type error! No possible type T! return 0; }
A program is an sequence of global variables, function declarations, then a special
function called main. Since sequences are ordered, all names are declared before use!
In C, main usually exits with return 0. Global variables tend to pollute
the namespace and are more trouble than they're worth, so we shall ignore them
–however they are already included by default since assignment is a top-level construct.
Incidentally, function declarations with no arguments may be used to simulate global
constants.
Note that C does not permit function overloading.
Moreover, C uses the same namespace for methods as well as simple variables
–which in is not the case in, say, Java which permits naming a method f and a
variable f to obtain the valid invocation f(f)!
Details
int it(int x){ return x; } int it = 5; int maybe = it(it);
4.1.1 Effectful Expressions
In C, any expression followed by a semicolon is a statement: The value of the expression is simply ignored when it is used as a statement.
Conversely, statements may be regarded as an effectful expression.
For example, assignment x ≔ E assigns the value of E to x and returns the value of E.
Whence, the notion of
Details
void continued_assgns() { int x = 1, y = 2, z = 4; //@ assert x == 1 && y == 2 && z == 4; x -= y += z; // Assignments are right-associative! //@ assert z == 4 && y == 2+4 && x == 1-(2+4); //@ assert z == 4 && y == 6 && x == -5; }
4.2 An Example Functional Contract
Look at the definition of abs below and notice:
- Frama-C contracts are comments beginning with an
@symbol and concluded with a;symbol. - The post-condition is introduced with the
ensuresclause; which may contain the\resultkeyword to refer to the returned value of the method. - We may combine multiple
ensuresclauses by using conjunction&&, or have them on separate lines. We may also use implication==>, disjunction||, negation!, value equality==, and Boolean equivalence<==>.- Notice that implication:
A ==> Binforms that whenAis true then so isB, and ifAis false then we don't care and consider the whole thing to be true.
- Notice that implication:
- Notice that we may name our conditions, which is helpful to remind us of their purpose as well as being helpful in the frama-c output.
/*@ ensures always_nonnegative: \result >= 0; @ ensures val > 0 ==> \result == val; @ ensures val < 0 ==> \result == -val; */ int abs(int val) { return (val < 0) ? -val : val; }
Pressing F9, you will notice that we are also checking for runtime errors by using the RTE plugin
whose goal is to ensure the program cannot create runtime errors such as integer overflow,
invalid pointer dereferencing, division by 0, etc.
In our case, we have runtime problems that do not crash but instead produce logical errors:
The return value of abs is not positive! Indeed, in addition to the above block, add focus
to the following block by removing the prefix -not, then run the code with F6 to see the output.
–Remember to undo this alteration when you're done, otherwise the next invocation to frama-c
will take a while dealing with printf!
#include<stdio.h> // for IO #include<limits.h> // bounds on integers #include<math.h> int main() { // Our implementation is faulty.. printf(" INT_MIN = %d\n", INT_MIN); printf("abs(INT_MIN) = %d\n\n", abs(INT_MIN)); printf(" INT_MIN + 1 = %d\n", INT_MIN+1); printf("abs(INT_MIN + 1) = %d\n\n", abs(INT_MIN+1)); // Using standard library works.. printf("fabs(INT_MIN) = %.0f", fabs(INT_MIN)); return 0; }
The WP plugin forms the necessary proof obligations to ensure the program meets its
specification, simplifies them using a module called Qed, then asks a prover such as
Alt-Ergo whether the obligation is provable or not. Sometimes a property is not
verified for two possible reasons:
- There is not enough information –e.g., given assumptions– for the proof to go through.
- The proof search timed-out –which can be configured.
4.2.1 Exercise: Fixing abs
- Remove focus from the
main()code block. - Go back to the Incomplete Absolute Value code block.
- Include the limits header file.
- Add
@ requires INT_MIN < val;to the top of the function contract. - Check that the contract passes by pressing
F9. - What bound conditions can you place on the result?
- Experiment by altering the conditions or method body.
4.2.2 Behaviours
Notice that our absolute value function has two disjoint behaviours –depending on whether the input is positive or negative. Each behaviour has some assumptions and some conclusions. Moreover, our behaviours are
disjoint: Every input can only satisfy the assumptions of at most one of the behaviours. As such, the program is ‘deterministic’: At most one of the behaviours is possible. –The program is really a relation and this ensures it is univalent; i.e., a partial function–complete: Every input satisfies the assumptions of at least one of the behaviours. As such, the program is ‘total’: At least one behaviour is possible. –The program is really a relation and this ensures it is total; i.e., defined on all inputs–
We expressed our behaviours in the forms ensures ⟨assumptions⟩ ==> ⟨consequences⟩.
However this can get unruly when there are many assumptions and many consequences.
Moreover, expressing disjointness is tedious and error-prone even in our little
example, below, where it becomes the assertion: (val < 0 && val >= 0) <==> \false.
As such there is the alternative behavior syntax –note the American spelling!
Using this syntax, we can ask WP to verify that the behaviours are complete or disjoint,
or both.
#include<limits.h> /*@ requires INT_MIN < val; @ ensures always_nonnegative: \result >= 0; @ @ behavior positive_input: @ assumes val > 0; @ ensures \result == val; @ @ behavior negative_input: @ assumes val <= 0; @ ensures \result == -val; @ @ complete behaviors; @ disjoint behaviors; */ int abs(int val) { return (val < 0) ? -val : val; }
Details
Exercise Replace each FixMe so that the program is proven correct.
#include "Prelude.c" /*@ requires INT_MIN < val; @ ensures always_nonnegative: \result >= 0; @ ensures Exercise: @ FixMe // Positive case @ && (val <= 0 ==> \result == -val) // Negative or 0 case @ && !(val > 0 && val <= 0) // Disjointness condition @ && FixMe // Completeness condition @ ; */ int abs(int val) { return (val < 0) ? -val : val; }
Exercise Replace each FixMe with the weakest proposition so that the program is proven correct.
#include "Prelude.c" /*@ requires INT_MIN < val; @ ensures always_nonnegative: \result >= 0; @ @ behavior positive_input: @ assumes Exercise: FixMe; @ ensures \result == val; @ @ behavior negative_input: @ assumes Exercise: FixMe; @ ensures \result == -val; @ @ complete behaviors; // Frama-C complain here, but please fix the “Exercises”! */ int abs(int val) { return (val < 0) ? -val : val; }
Exercise Replace each FixMe with the strongest proposition so that the program is proven correct.
#include "Prelude.c" /*@ requires INT_MIN < val; @ ensures always_nonnegative: \result >= 0; @ @ behavior positive_input: @ assumes Exercise: FixMe; @ ensures \result == val; @ @ behavior negative_input: @ assumes Exercise: FixMe; @ ensures \result == -val; @ @ disjoint behaviors; */ int abs(int val) { return (val < 0) ? -val : val; } // This program passes 100%, but that is because it assumes false, the “FixMe”.
4.3 Proving is Programming
In this section we step back a little to get more comfortable with requires
preconditions and ensures postconditions. Moreover, we use this time to remind
ourselves of some elementary logic. After all, we use logic to express properties
and hope Frama-C can verify them.
In some sense false, true behave for the 𝔹ooleans as -∞, +∞ behave for the ℕumbers.
| 𝔹ooleans | ℕumbers |
| p ⇒ true | n ≤ +∞ |
| false ⇒ p | -∞ ≤ n |
| Implication ⇒ | Inclusion ≤ |
| Conjunction ∧ | Minimum ↓ |
| Disjunction ∨ | Maximum ↑ |
Using this correspondence we can rephrase the “Golden Rule” p ∧ q ≡ p ≡ q ≡ p ∨ q as the following trivial property x ↓ y = x ≡ y = x ↑ y –“The minimum of two numbers is the first precisely when the second is their maximum.” Neat Stuff!
Details
Ex falso quodlibet From false, anything follows: false ⇒ p, for any p.
Edit FixMe in the following snippet so that it ensures the result is equal to 42.
#include "Prelude.c" /*@ requires uhOh: a < 0 && a > 0; @ ensures what: Exercise: FixMe; */ int id(int a){ return a;}
Right Identity of Implication Everything implies true; that is p ⇒ true, for any p.
Edit FixMe in the following snippet so that it there are no errors.
#include "Prelude.c" /*@ requires Exercise: FixMe; // <-- Change this false positive. @ ensures \true; */ int id(int a){ return a; }
Exercise
Replace each FixMe with the weakest possible predicate so that it passes.
#include "Prelude.c" /*@ requires \true; @ ensures UpperBound: a <= \result && b <= \result; @ ensures Exercise: Selection1: FixMe ==> \result == b; @ ensures Exercise: Selection2: FixMe ==> \result == a; @*/ int max(int a, int b) { return a < b ? b : a; }
Conversely, that maximum is the least upper bound, x ≤ z ∧ y ≤ z ≡ x ↑ y ≤ z, corresponds to the characterisation of disjunction (p ⇒ r) ∧ (q ⇒ r) ≡ (p ∨ q) ⇒ r –incidentally this is also known as “case analysis” since one proves p ∨ q ⇒ r by providing a proofs that if p ∨ q is true due to p then with p in hand we need to show r, and likewise if p ∨ q is true due to q.
Exercise
Replace FixMeCode with the least amount of code so that the following passes.
#include "Prelude.c" #define max(a,b) (a < b ? b : a) // Ignore me. /*@ requires max(a, b) <= c; @ ensures a <= c && b <= c; @*/ void case_analysis(int a, int b, int c) { FixMeCode; }
4.4 Maintaining The Sequence Rule
Since function calls may alter memory state, the computation of a term may now
not only produce a value, as before, but also alter the state altogether.
( Foreshadowing: The assigns ACSL keyword! )
Since a return interrupts executation, the sequence computation rule
wp (S₁;S₂) = wp S₁ ∘ wp S₂ is no longer valid when the execution of S₁ causes the
execution of a return thereby necessitating that S₂ is not executed.
As we have already seen, we keep the rule valid by simply defining wp U R ≡ true
for any unreachable code U –as is S₂ when S₁ has a return.
That is, unreachable assertions are always ‘true’: They are never in a memory state, and so cannot even be evaluated, let alone be false!
int main() { goto End; //@assert my_cool_nonsense: 0 == 1; // This is unreachale but ‘true’. End: return 0; }
Likewise with infinite loops,
int main() { while(1 > 0); //@assert my_cool_nonsense: 0 == 1; // This is unreachale but ‘true’. return 0; }
That is, Frama-C considers ‘partial correctness’: A specification is satisfied, provided it terminates.
In addition, since imperative expressions can modify memory, considerations must be
given to the fact arguments of a function are evaluated from left to right.
For example, suppose x,y are imperative constructions yield integers, then
x + y and y + x are not guaranteed to produce the same behaviour!
Details
#include<stdio.h> // for IO int f(){ printf("\nf(): Hello with Four!"); return 4;} int g(){ printf("\ng(): Hello with Three!"); return 3;} int main() { int result; // The output to the screen changes, // even though the *value* of result does not. result = f() + g(); printf("\n---"); result = g() + f(); return 0; }
The C language does not specify the order of evaluation of function arguments –albeit it is usually left-to-right–, and it is up to the programmer to write programs whose result does not depend on the order of evaluation.
Exercise: Produce a Frama-C checked variant of this example.
Remember to remove all printf's!
4.5 Passing Arguments by Value and by Reference
Applying the definition of wp to the body of the following swap gives us
wp swap = id, thereby demonstrating that this swap does not change the
values of two variables!
void swap(int a, int b){ int c; c = a; a = b; b = c; }
The default mechanism of argument passing is that of pass by value:
Only values are sent to function bodies, which cannot alter the original variables.
Indeed, what should swap(x+y, 2) perform if it were to “alter the given variables”?
To say that two distinct variables share the same location in memory requires us to formally introduce a notion of location that variables may reference. Rather than introduce a new such type, C makes the convention that certain numeric values act –possibly dual roles– as reference locations.
Hence we can associate variables to references which are then associated to values. That is, a state now consists of two pieces: An environment mapping variables to references and a memory state mapping references to values. The key insight is that the environment may be non-injective thereby associating distinct variables to the same reference thereby permitting them to alter the shared value. Incidentally, the shared value can be thought of as a buffer for message passing between the two variable agents. Neato!
In C, passing by reference is not a primitive construct, but it can be simulated.
The type of references that can be associated with a value of type T in memory
is written T* in C. Incidentally, the dereference operator is written * in C.
For example, in environment u ↦ r₁ and memory state r₁ ↦ r₂, r₂ ↦ 4 we have
that u has value r₂ whereas *u has value 4. That is, u is a reference value at location r₁
having contents r₂, which when dereferenced refer to the value contained in location r₂
which is 4.
The reference associated with variable x in a C environment is written &x.
E.g., in environment x ↦ r and memory state r ↦ 4, the value of x is the integer 4
whereas the value of &x is the reference r. Moreover, the value of *&x is the integer 4.
&_ : ∀{T} → Variable T → Reference T -- “address of”
*_ : ∀{T} → Reference T → T -- “value of”
-- Using ‘value equality’:
Inverses: ∀ a : Var T. *&a ≈ a
Inverses: ∀ r : Ref T. &(*r) ≈ r
Details
void understanding_references() { int a = 4; // integer a refers to 4 int* x = &a; // integer reference x refers to the location of a // Facts thus far // //@ assert a_is_a_number: a == 4; //@ assert x_points_to_a: *x == a == 4; //@ assert x_is_a_location: x == &a; // The inverse law: a == *(&a). // //@ assert x_points_to_a: *x == a == 4; //@ assert x_is_a_location: x == &a; //@ assert equals_for_equals: *(&a) == *x == a; // The inverse law: &(*x) == x // //@ assert x_points_to_a: *x == a == 4; //@ assert x_is_a_location: x == &a; //@ assert equals_for_equals: &(*x) == &a == x; }
If t is an expression of type T* then the C language has the assignment
construct *t = u: The reference of t is now associated with the value
of u. The notation alludes to this executional behaviour:
The contents of t, i.e., *t, now refer to the value of u.
For example, *&x = u has the same behaviour as the assignment x = u.
Details
#include<stdio.h> // for IO // x and y themselves cannot be assigned to: They're constant. // I.e., assignments “x = t” are forbidden, but “*x = t” are permitted. // This makes the compiler complain if we accidently made that assignment instead. // // However, “const int* x” works in the opposite: x=t okay, but not *x=t. // Declaration “const int* const x” prevents both types of assignments. void swap(int* const x, int* const y) { int z; z = *x; // z gets the value referenced to by x *x = *y; // the location x references now gets the value referenced by y *y = z; // the location y references now gets the value z } int main() { int x = 5, y = 10; swap(&x, &y); // Note that the function is applied to the references. printf("x = %d, y = %d", x , y); return 0; }
4.5.1 Dangling References: Segmentation Faults
In C, we may look for references that do not exist: C removes from memory the reference associated with a variable when that variable is removed from the environment.
Details
#include<stdio.h> // for IO int* f(const int p) { int n = p; return &n; // n only exists locally, // whence its reference is removed when it no longer exists. } int main() { int* u = f(5); int* v = f(10); printf("u = %d, v = %d", *u , *v); // Segmentation fault! return 0; }
The compiler gives us
warning: function returns address of local variable [-Wreturn-local-addr].
We may thus turn on that warning –and all warnings really!– so that it becomes
an error at compile time.
Since we used a reference that is not declared in memory, C does not produce a compile error but the runtime result is unpredictable. Execute the above snippet to see different kinds of segmentation fault codes.
4.5.2 Pointers in ACSL
The \old function is a built-in logical operation of ACSL.
It can only be used in the post-condition and it denotes the value before execution
of the method body. If we want to access the value at a particular memory state,
we simply refer to a label at that time frame using the \at construct –see below.
/*@ requires \valid(a); @ ensures *a == \old(*a); @ ensures \at(*a, Post) == \at(*a, Pre); // Alternative way to say the same thing. */ void at_example(int *a) { int tmp = *a; AfterLine1: *a = 23; AfterLine2: *a = 42; AfterLine3: *a = tmp; // We are now in the memory state after the fourth line. // // Here are some true facts about the memory states: //@ assert *a == \at(*a, Pre); // Current value of *a is same as before method. //@ assert \at(*a, Here) == \at(*a, Pre); // More explicitly. //@ assert 42 == \at(*a, AfterLine3); //@ assert 23 == \at(*a, AfterLine2); }
Besides user-defined labels, \at can also be used with the built-in labels:
Pre: Value before function call.Post: Value after function call. –Can only be used in the post-condition.Here: Value at the current program point. –This' the default for stand-alone variables.
Whereas \old can only be used in the post-condition, \at can be used anywhere.
Notice that we used the built-in \valid to ensure that access to pointers is safe
–i.e., pointing to a real memory location– thereby avoiding runtime errors.
We may also write \valid(p + (l .. u)) to express the validity of pointers
p + i for l ≤ i ≤ u –this will be helpful when working with arrays.
Moreover, when working with constant, non-mutable, pointers, or if we wish to
be more accurate, we may use \valid_read(p) to express that the pointer p is valid for
read-access only –no writing permitted.
4.6 Side-effects: assigns
Since methods may alter state, thereby producing side-effects, it becomes important
to indicate which global and local variables a method assigns to
–that way its effects are explicit. We use the assigns clause to declare this.
Unless stated otherwise, WP assumes a method can modify anything in memory;
as such, the use of assigns becomes almost always necessary.
When a method has no side-effects, thereby not assigning to anything, we may
declare assigns \nothing.
/*@ requires \valid(a) && \valid(b); // @ assigns *a, *b; @ ensures *a == \old(*b); @ ensures *b == \old(*a); */ void swap(int *a, int *b) { int tmp = *a; *a = *b; *b = tmp; }
Notice that the following block fails to prove all goals
–comment out the assigns clause below and re-check … still no luck!
This can be fixed by un-commenting the assigns clause above.
int h = 12; // new global variable! //@ assigns \nothing; // In particular, this method does not alter “h”. int main() { int a = 1; int b = 2; //@ assert h == 12; swap(&a, &b); //@ assert h == 12; return 0; }
Finally it is to be noted that assigns do not occur within a behavior
–it occurs before by declaring all variables that may be altered, then
each behavior would include a clause for the unmodified variables by indicating
their new value is equal to their \old one.
4.7 Pointer Aliasing: separated
The raison d'être of pointers is to be able to have aliases for memory locations. When the pointers refer to simple data, we may act functionally in that we copy data to newly allocated memory locations. However, sometimes –such as when we program with linked lists– copying large amounts of data is unreasonable and we may simply want to alter given pointers directly. When the given pointers are identical then an alteration to one of them is actually an alteration to the rest!
When we program with lists, we shall see that if we catenate two lists by altering the first to eventually point to the second then it all works. However, if we catenate a list with itself then the resulting alteration is not the catenation of the list with itself but instead is an infinite cycle of the first list! –We'll see this later on.
Here is a simpler example,
#include<limits.h> /*@ requires \valid(fst) && \valid_read(snd); @ requires no_flow: INT_MIN <= *fst + *snd <= INT_MAX; // @ requires \separated(fst, snd); @ assigns *fst; @ ensures uhOh: *fst == \old(*fst) + *snd; */ void increment_first_by_second(int *fst, int const *snd) { *fst += *snd; }
Notice since we're only assigning to *fst, we need not explicitly state
ensures *snd == \old(*snd). However, in the event that fst and snd both point
to the same memory location, then we actually are assigning to both!
As such the final ensures is not necessarily true either!
We need to uncomment the separated declaration: The memory locations are distinct.
Notice that in the final call below, since the pre-condition to
increment_first_by_second fails, we have breached its contract and therefore
no longer guarenteed the behaviour it ensures.
Since the contract does not tells what happens when we breach it, anything is possible
and so anything is “true”!
int main() { int life = 42, universe = 12; int *this = &life; int *new = &universe; //@ assert *this == 42 && *new == 12; increment_first_by_second(this, new); //@ assert *this == 42 + 12 && *new == 12; // Yay! int *that = &life; // uh-oh! //@ assert *this == 54 && *that == 54; increment_first_by_second(this, that); //@ assert *this == 54 + 54 && *that == 54; // Nope...? //@ assert 1 == 0; // Notice everything is now “true”! return 0; }
We may invoke \separated(p₁, …, pₙ) to express the pointers pᵢ should refer to distinct
memory locations and therefore are non-overlapping.
4.8 Functional Composition
As a matter of abstraction, or separation of concerns, a program may be split up into an interface of declarations –a ‘header’ file– and an implementation file. Frama-C permits this approach by allowing us to use a specification of a declared method, which it assumes to be correct, and so we need to verify its precondition is established whenever we call it. In some sense, for proof purposes, this allows us to ‘postulate’ a correct method and use it elsewhere –this idea is very helpful when we want to use an external libary's methods but do not –or cannot– want to prove them.
Details
#include<limits.h> /*@ requires val > INT_MIN; @ assigns \nothing; @ ensures always_non_negative: \result >= 0; @ ensures non_negative: 0 <= val ==> \result == val; @ ensures negative: val < 0 ==> \result == -val; @ */ int abs(int val); /*@ assigns \nothing; @ ensures UpperBound: a <= \result && b <= \result; @ ensures Selection1: a <= b ==> \result == b; @ ensures Selection2: b <= a ==> \result == a; @*/ int max(int a, int b); // Uncomment this to observe proof obligations failing. // // int max(int a, int b){ return 5; } /*@ requires inherited_from_abs: a > INT_MIN && b > INT_MIN; @ assigns \nothing; @ ensures always_non_negative: inherited_from_abs: \result >= 0; @ ensures upper_bound: inherited_from_max: \result >= a && \result >= -a // ≈ result ≥ |a| && \result >= b && \result >= -b; // ≈ result ≥ |b| @ ensures selection: inherited_from_max: \result == a || \result == -a || \result == b || \result == -b; */ int abs_max(int a, int b) { return max(abs(a), abs(b)); }
If we press F8, the frama-c gui shows green bullets for the declarations'
specifications. They have no implementation and so are assumed to be true.
Then the abs_max operation ‘inherits’ the preconditions and postconditions of
the methods it calls along the variables it uses.
5 Records
Thus far we have only considered built-in types, we now turn to considering user-defined types that are more complex and are composites of simpler types by using the record construct.
- Record ≈ Tuple with named fields
A tuple x = (x₀, x₁, …, xₙ) is a function over the domain 0..n, but in programming
the domain is usually of named fields, labels, and then it is called a record.
E.g., {name = "Jasim", age = 27, language = "ar"} is a record.
In the case that the labels are numbers, we obtain the notion of an array.
In other languages, this may be known as a class.
In Haskell this is the data keyword with ‘record syntax’,
and in Agda we may go on to use the record keyword.
C records are known as structures and they are just a list of
labels with their types. In using struct types, the struct
keyword must precede the type name in all declarations.
struct Pair { int fst; int snd; }; // Note that “struct” always precedes the type name “Pair”. // Structs are passed in by value: They are copied locally. // //@ assigns \nothing; void doesNothing(struct Pair p) { p.fst = 666; } // As usual, we use pointers to pass values by reference. // /*@ requires \valid(p); @ assigns (*p).fst; */ void woah(struct Pair* p) { (*p).fst = 313; }
#include<stdio.h> // for IO int main() { struct Pair p; // no initalisation // Composite type without a name. struct {int one; int two;} q; // Initialisation with declaration. struct Pair r = {11, 13}; // Note that in C, non-initialised variables have “arbitrary” values // which may change according to each new compilation! printf("\n p = ⟨fst: %d, snd: %d⟩", p.fst, p.snd); // Set only first field. p.fst = 3; printf("\n p = ⟨fst: %d, snd: %d⟩", p.fst, p.snd); // Zero-out all fields. struct Pair s = {}; printf("\n s = ⟨fst: %d, snd: %d⟩", s.fst, s.snd); // Invoke functions doesNothing(s); printf("\n s = ⟨fst: %d, snd: %d⟩", s.fst, s.snd); woah(&s); printf("\n s = ⟨fst: %d, snd: %d⟩", s.fst, s.snd); return 0; }
5.1 Allocation of a Record
- Recall that a variable declaration associates the variable with a reference to the variable in memory –i.e., it's address–, moreover this reference is associated a value for the variable.
- Record variables declared without a value are given the special default value
null. - In Java, a record variable's reference is not directly associated with a record in memory!
It is usually associated with
nullor another reference.
To associate a record with a variable, we need to create memory large enough to contain the record
contents. Some languages use the keyword new to accomplish this task: Create a new reference
and associated it with the record variable being defined.
For example, in Java,
class Pair
{
int fst;
int snd;
}
Pair p = new Pair();
The resulting environment is p ↦ r and the resulting memory state is
r ↦ r', r' ↦ {fst = 0, snd = 0}. Note that default values are used.
- A reference that was added to memory by the construct
newis called a cell. - The set of memory cells is called a heap.
- The operation that adds a new cell to the memory state is called allocation.
Interestingly in C the creation of records does not allocate cells and so there
is no need for the new keyword. Indeed record variables cannot ever have the value null.
C directly associates a variable with a reference which has the record contents as its value.
That is, C has one less level of indirection than is found in Java.
E.g., struct Pair p = {2, 3}; gives us environment p ↦ r and memory state r ↦ {fst = 2, snd = 3},
whereas Java would have p ↦ r′ in the environment and r′ ↦ r additionally in the memory state
That is to say, records in Java correspond to references to records in C
and so Java access notation r.f is rendered in C as (*r).f.
Remember that references are themselves first-class values and it is possible for a reference to be associated to another reference.
5.2 The Four Constructs of Records
Records are usually handled using four constructs:
- Defining a record type; e.g., using
classorstruct. - Allocating a cell; e.g., using
newormalloc. - Accessing a field; e.g.,
myRecord.myField. - Assigning to a field; e.g.,
myRecord.myField = myValue.
Understanding records in a language is thus tantamount to understanding
these fundamental basics. E.g., in functional languages, assignment to a field
is essentially record copying or, more efficiently, reference redirection.
Incidentally, neither Haskell nor Agda make use of the new keyword:
Declarations must be accompanied by initialisation which indicate the need
for cell allocation –consequently there is no need for a null value.
The use of new may be used for careful efficiency optimisations,
or memory management –which is rarely brought to the forefront in functional languages.
The act of assigning to each field of a record is so common that they are usually placed into a so-called constructor method.
5.3 Sharing, Equality, & Garbage
5.3.1 Assignment
Suppose x and y are variables of type Pair, with environment and memory state:
locations = x ↦ r₁, y ↦ r₂
values = r₁ ↦ r₃, r₂ ↦ r₄, r₃ ↦ {fst = 3, snd = 5}, r₄ ↦ {fst = 7, snd = 9}
Then assignment y ≔ x results in:
locations = x ↦ r₁, y ↦ r₂
values = r₁ ↦ r₃, r₂ ↦ r₃, r₃ ↦ {fst = 3, snd = 5}, r₄ ↦ {fst = 7, snd = 9}
-Change Here-
That is, the value of x is computed which is the reference r₃
–since value (location x) ≈ value r₁ ≈ r₃–
and we associate this value with the location of y, that is, reference r₂.
Notice that now no variable has the value of r₄ and so it is considered garbage
in our state. Moreover, nothing can get to it since values are only associated with
locations, none of which have address r₄. Hence there is no observable affect to
their absence or presence. We want to recycle the physical memory
or else we would quickly run out of memory. A garbage collector is an automated
system that collects and recycles such cells. Older languages like C do not
have such a system and so memory must be managed by hand.
Anyhow, henceforth x and y share the values of the record thereby all alterations,
through either variable, are observable by the other.
Since x and y are reference values, the assignment makes x == y a true statement
since they share the same cell. This is known as physical equality.
Sometimes we wish for two variables to share a single integer, which may
not be possible with built-in types, but can be accomplished by using wrapper record types:
Records that have a lone single field. This idea of `boxing up' primitive types
allows us, for example, to define functions with arguments that are passed by reference
thereby modifying their arguments; such as the swap function that swaps the contents of its
arguments.
5.3.2 Copy
If we instead execute y.fst ≔ x.fst; y.snd ≔ x.snd
Then the resulting state is:
locations = x ↦ r₁, y ↦ r₂
values = r₁ ↦ r₃, r₂ ↦ r₄, r₃ ↦ {fst = 3, snd = 5}, r₄ ↦ {fst = 3, snd = 5}
-Change Here-
In this case, any alteration to x's values are not observable by y.
Moreover, in this case, all fields are equal and so we have x and y
are structurally equal. This notion is sometimes called equals method
and the previous is equals equals (==).
5.4 Arrays
Arrays are essentially records whose labels are numeric and all labels have the same type. The number of fields of an array is determined during allocation of the array, and not during the declaration of its type, as is the case with records. This trade-off makes arrays more desirable in certain contexts.
The fields are usually numbered 0 to n-1, where n is the number of fields.
Once an array is allocated, its size cannot be changed. –Stop & think: Why not?
- Arrays of type
Tare denoted byT[]in C/Java.- Matrices, or arrays of arrays, are denoted by
T[][]with access byT[i][j].
- Matrices, or arrays of arrays, are denoted by
C arrays, like records, are not allocated. Consequently, their size cannot be determined by allocation and so must be a part of their type.
C arrays of type T of length n are declared using the mixfix syntax: T x[n];
Each element of the array is arbitrary –with no designated defaults–
so it is best to initialise them. E.g., int x[10] = {}; sets all elements of
the array to 0.
#include<stdio.h> // for IO int makeFive(int x[], int length) { for(int i=0; i != length; i++) x[i] = 5; } int main() { int x[3] = {}; printf("\n x = [%d, %d, %d]", x[0], x[1], x[2]); makeFive(x, 3); printf("\n x = [%d, %d, %d]", x[0], x[1], x[2]); return 0; }
However, C arrays differ from C records in that array variables are actually references that are associated in memory with an array. Consequently, array arguments to methods are automatically pass by reference!
Moreover this means the assignment t[k] = u works in a rather general sense:
t suffices to be any expression whose value is a reference associated in memory
with an array.
6 Arrays – \forall, \exists
Arrays are commonly handled using loops; let's look at some examples.
/*@ requires 0 < N; @ requires \valid_read(array + (0 .. N - 1)); // N is the length of the array @ @ assigns \nothing; @ @ behavior found_element: @ assumes \exists integer i; 0 <= i < N && array[i] == element; @ ensures 0 <= \result < N; @ @ behavior did_not_find_element: @ assumes \forall integer i; 0 <= i < N ==> array[i] != element; @ ensures \result == N; @ @ disjoint behaviors; @ complete behaviors; */ int linear_search(int* array, int N, int element) { int n = 0; /*@ loop assigns n; @ loop invariant 0 <= n <= N; @ loop invariant not_found_yet: \forall integer i; 0 <= i < n ==> array[i] != element; @ loop variant N - n; */ while( n != N && array[n] != element ) n++; return n < N ? n : N; }
Some remarks are in order.
\valid_read(array + (0 .. N - 1))ensures that the memory addressesarray + 0, ..., array + N-1can be read –as discussed when introducing\valid.- The loop continues as long as we have not yet found the element.
- As such, every index thus far differs from the element sought after.
- That is, forall index i in the array bounds, we have array[i] ≠ element.
- This invariant is stated using the
forallsyntax.
- The variable naming
n, Nis intended to be suggestive: When n = N then we have traversed the whole array.- We began at 0 and are working upward to N.
- At each step, we traverse the array by one more item thereby decreasing the amount of items remaining –which is N - n.
- If it is provable that some index contains the desired element, then in that case our program ensures the output result is a valid index.
- The ACSL type
integeris preferable to the C typeintsince it is not constrained by any representation limitations and instead acts more like its pure mathematical counterpart ℤ.
It is important to note that the universal ‘∀’ uses ==> to delimit the
range from the body predicate, whereas the existential ‘∃’ uses &&
–this observation is related to the “trading laws” for quantifiers.
\forall type x; r(x) ==> p(x) |
Every element x in range r satisfies p |
\exists type x; r(x) && p(x) |
Some element x in range r satisfies p |
Notice the striking difference between
the \exists integer x; \false && even x
–which is unprovable since false is never true!–
and \exists integer x; \false ==> even x
–which can be satisfied by infinitely many x, since false implies anything.
Of course we could start at the end of the array and “work down” until
we find the element, or otherwise, say, return -1. Let's do so without using
a new local variable n.
Details
#include "Prelude.c" /*@ requires 0 < N; // @ requires Exercise: read access to a[0], ..., a[N-1]; @ // @ assigns FixMe; @ @ behavior found_element: @ assumes Exercise: FixMe; // “element ∈ array” @ ensures Exercise: FixMe; // Output is valid index in array @ @ behavior did_not_find_element: @ assumes Exercise: FixMe; // “element ∉ array” @ ensures \result == -1; @ @ disjoint behaviors; @ complete behaviors; */ int linear_search_no_local(int* array, int N, int element) { /*@ loop assigns N; @ loop invariant 0 <= N <= \at(N, Pre); // @ loop invariant not_found_yet: Exercise: FixMe; // @ loop variant Exercise: FixMe: 666; */ while( 0 != N && array[N-1] != element ) N--; return N - 1; }
Details
#include "Prelude.c" /*@ requires Exercise: FixMe; // array[0], ..., array[N-1] are accessible @ requires element < INT_MAX; @ assigns array[0 .. N-1]; @ @ ensures Exercise: all_array_equals_element: FixMe; */ void make_constant(int* array, int N, int element) { /*@ loop assigns N, array[0 .. \at(N,Pre)-1]; @ loop invariant range_on_N: FixMe; @ loop invariant constant_so_far: FixMe; @ loop variant N; */ for (; 0 != N; N--) array[N-1] = element; }
Notice that the invariants are getting way too long –and worse: Repetitive! We can abstract common formulae into more general and reusable shapes by declaring them as ACSL logical functions –keep reading!
On an unrelated note, sometimes we try to prove a program that we just coded incorrectly, so if things are going nowhere then maybe try a few tests to ensure you're on the right track.
7 Recursion
The definition of wp for function calls is correct provided the function body
itself only contains invocations to previously defined functions?
What about recursive function definitions: Definitions invoking the function being defined or invoking functions that invoke functions that eventually invoke the function currently being defined?
Since invocations are delegated to the state, which handles all defined names, we may invoke whatever function provided its name is found. Since C requires names to be declared before use, we may have mutually recursive functions by ‘prototyping’: Declaring the function signature, then at some point providing the actual implementation.
Details
#include<stdio.h> // for IO #include<stdbool.h> bool odd(int); // protoyping the odd function bool even(int n) // using odd here, even though it's not yet defined { if (n == 0) return true; else return odd(n - 1); } bool odd(int n) { if (n == 0) return false; else return even(n - 1); } int main() { printf("\n 7 is even? ... %d", even(7)); printf("\n 7 is odd? ... %d", odd(7)); return 0; }
Anyhow, e.g., void f(int x){ f(x); } has the definition of wp f(x) using the value of wp f(x)
and so is circular. How can this be avoided?
Note that a recursive definition is not just a definition that uses the object which it
is defining. Otherwise, the previous f might as well have been the definition of
the factorial function that on input x simply invokes itself; then again it could
have been any function!
Details
We generally think of recursive definitions as definitions by usual ℕ-induction, however
this is not absolutely true.
E.g., the following function at n not only relies on
values on smaller inputs but also on values at larger inputs to compute the value at n!
#include<stdio.h> // for IO int iterations = 0; #define RETURN(i, n) { printf("\n **Computed value for input %d is %d**", i, n); \ iterations++; return n; } // Uses smaller as well as larger values just to compute current value! int f(int n) { printf("\n Computing value for: %d", n); if (n <= 1) RETURN(n, 1) if (n % 2 == 0) RETURN(n, 1 + f(n / 2)) else RETURN(n, 2 * f(n + 1)) } int main() { f(12); printf("\n\n The function was invoked for a total of %d times!", iterations); return 0; }
Similarly the Ackermann function is a recursive function that has been proven to be undefinable using only nested definitions by ℕ-induction. ( However, since ℕ×ℕ is well-ordered, it is a valid definition. )
We may try to remove recursive calls by replacing every recursive call with the function body itself, which then has a new recursive call. We may continue to expand forever by replacing recursive calls with the original function body. The “result” will be an non-recursive program that is infinitely long.
Thus, recursive programs, like while loops, are a means of expressing infinite
programs and, like while loops, they introduce the possibility of non-termination.
As for while loops, we can approximate the infinitely long non-recursive program
by simply giving-up on the n-th expansion, not making any more recursive calls.
Essentially, we do n recursive calls then give-up if the program has not completed.
Hence, we again consider the limit.
7.1 Recursive Definitions and Fixed Point Equations
A recursive function such as the factorial function can be seen as
an equation where the unknown variable is the function currently being defined.
For example, the factorial function is the unique partial function f satisfying
the equation
f ≈ (x ↦ if x ≈ 0 then 1 else x * f(x-1))
This equation has the form f ≈ F(f), so it is a “fixed point equation”.
Since recursive functions may not terminate, the functions they describe
are partial. It can be proven that any fixed point equation always has
at least one solution; i.e., it defines at least one partial function on the integers.
For example, the equation f ≈ (x ↦ 1 + f(x)) corresponding to
int loop(int n){ return 1 + loop(n); }
Has one solution: The empty function, which is not defined on any input.
The set of possible solutions can be ordered by inclusion of their graphs and so one of them is the smallest. Incidentally, this least solution is also obtained by the aforementioned limit!
E.g., every function is a solution to the equation f ≈ (x ↦ f x).
7.2 Programming without Assignment –the Functional Core
Notice that the factorial function can be written without using assignments:
Details
/*@ axiomatic Factorial @ { @ logic integer factorial(integer n); @ @ axiom fact_zero: \forall integer n; factorial(0) == 1; @ @ axiom fact_succ: \forall integer n; 0 <= n @ ==> factorial (n + 1) == n * factorial (n); @ @ axiom fact_monotone : \forall integer m,n; 0 <= m <= n @ ==> factorial(m) <= factorial(n); @ } */
#include "Prelude.c" /*@ requires Exercise: FixMe; @ assigns \nothing; @ ensures Exercise: FixMe; */ int fact_imp(int n) { int r = 1; /*@ loop assigns i, r; @ loop invariant range_on_i: FixMe; @ loop invariant relationship_between_r_i_n: FixMe; @ loop variant FixMe: 666; */ for(int i = 1; i <= n; i++) r = r * i; return r; } // ≈ /*@ requires 0 <= n; @ requires factorial(n) <= INT_MAX; @ assigns \nothing; @ ensures \result == factorial(n); */ int fact_functional(int n) { if (n == 0) return 1; return n * fact_functional(n - 1); }
( Notice that ¬(i ≤ n)[i ≔ 1] ≡ n = 0 when considering n : ℕ. )
Hence if we remove assignments, then the memory state for computation is always empty and so sequences and loops become useless. We are left with only variable declarations, function calls, and the built-in operations. This is the functional core of the language and it is surprisingly as powerful as the imperative core. Why? Recall that a term, or statement, can be thought of as a (partial) function of its free variables; now the functions obtained this way using only the functional core are the same as those obtained by also using the whole of the imperative core! Note that omitting recursion falsifies this result.
8 Hehner's Problem
We have now covered enough material to tackle the problem posed
at the very beginning —that of whatDo.
Details
#include "Prelude.c" /*@ requires \valid(x) && \valid(y); requires 0 <= *x < 31; requires Exercise: FixMe; assigns *x, *y; ensures Exercise: FixMe; */ void whatDo(int* x, int* y) { if (*x == 0) { *y = 1; *x = 3; } else { *x -= 1; *y = 7; whatDo(x, y); *y *= 2; *x = 5; } }
Running a few test inputs, it can be seen that this program
sets y to be the power of x. Further testing may reveal interesting
issues when x and y refer to the same memory location!
Details
⟨x = 0, y = 0⟩ ↦ ⟨x = 3, y = 1⟩ ⟨x = 1, y = 2⟩ ↦ ⟨x = 5, y = 2⟩ ⟨x = 3, y = 4⟩ ↦ ⟨x = 5, y = 8⟩ ⟨x = 5, y = 6⟩ ↦ ⟨x = 5, y = 32⟩ ⟨x = 7, y = 8⟩ ↦ ⟨x = 5, y = 128⟩ ⟨x = 0, y = 99⟩ ↦ ⟨x = 3, y = 1⟩ x == y ⇒ Segmentation Fault
With this guidance in hand, we aim to axiomatise the power function:
/*@ axiomatic Pow @ { @ logic integer pow(integer b, integer n); @ @ axiom pow_zero: \forall integer b; pow(b, 0) == 1; @ @ axiom pow_one: \forall integer b; pow(b, 1) == b; @ @ axiom pow_homomorphism: \forall integer b, m, n; @ pow(b, m + n) == pow(b, m) * pow(b, n); @ @ axiom pow_monotone : \forall integer b,m,n; b >= 0 && 0 <= m <= n @ ==> pow(b,m) <= pow(b,n); @ } */
Notice that there are infinitely many solutions f to the equations
pow_zero: f(0) = 1pow_homomorphism: f(m + n) = f(m) * f(n)
Which ones? Since every natural number is of the form 1 + 1 + ⋯ + 0
the second requirement yields \\ f(n) = f (1 + 1 + ⋯ + 0) = f 1 * f 1 * ⋯ f 1 * f 0;
which by the first requirement simplifies to f(n) = (f 1)ⁿ.
Hence for any choice of number f(1) : ℕ, we obtain a function f
that satisfies these definitions. If we want f to be the n product of a number
b then we need to insist f 1 = b –which is just pow_one!
From the axioms, we obtain some useful lemmas.
//@ lemma pow_succ: \forall integer b, n; n >= 0 ==> pow(b, n + 1) == pow(b, n) * b; //@ lemma powNonNeg : \forall integer b,n; b >= 0 ==> n >= 0 ==> pow(b,n) >= 0; //@ lemma pow2bound : \forall integer n; 0 <= n < 31 ==> pow(2, n) < INT_MAX; /*@ lemma powPredT : \forall integer b,n,m; b >= 0 && n > 0 && pow(b, n) <= m ==> b * pow(b, n-1) <= m; */
With this setup, the reader should now be able to solve the FixMe's in whatDo
–which I've renamed to “hehner”, after the fellow who showed it as an example
in his excellent specifications and correctness text, A Practical Theory of Programming.
#include "Prelude.c" /*@ requires \valid(x) && \valid(y); requires 0 <= *x < 31; requires Exercise: FixMe; // Assuming \false, gives us anything! assigns *x, *y; ensures Exercise: FixMe; */ void hehner(int* x, int* y) { // Introduce a local for reasoning, to avoid having to write \at(*x, Pre). // ghost const int X = *x; // assert given: 0 <= X < 31; // assert taking_powers_with_monotonicity: 1 <= pow(2,X) <= INT_MAX; if (*x == 0) { // assert condition: X == 0; // assert taking_powers: pow(2,X) == 1; *y = 1; *x = 3; // assert *y == pow(2,X); } else { // assert condition: 0 < X < 31; // assert pow_with_monotonicity: 1 < pow(2, X) <= INT_MAX; // assert factoring: 2 * pow(2, X-1) <= INT_MAX; *x -= 1; *y = 7; hehner(x, y); // assert function_ensures: *y == pow(2, X - 1); // assert pow(2, X) == 2 * pow(2, X - 1); // assert pow(2, X ) ≤ INT_MAX; // assert 2 * pow(2, X - 1) ≤ INT_MAX; // assert y2_no_overflow: *y * 2 ≤ INT_MAX; *y *= 2; *x = 5; // assert our_goal: *y == pow(2, X); // assert incidentally: *y <= INT_MAX; } }
I've left the assert's since they may make the program proof more comprehensible
to the reader –yet notice that I did not use @ and so they are not visible,
nor necessary, to Frama-C.
9 Advanced Data Structures
This is what I have so far, yet I look forward to including material utilising linked lists as well as making more of the Curry-Howard Correspondence.
Anyhow, I hope you've enjoyed yourself and hopefully learned something neat! Byebye!
10 The Underlying Elisp
The following utilities are loaded when this file is opened.
After the first time the file InteractiveWayToC.el is created and this section
may be deleted, or COMMENT-ed, as it is loaded in the footer section at the end of this file.
- Make some changes, look at them with
f7.- Or execute with
f6if there is amainmethod.
- Or execute with
- Check your progress with
f9, within Emacs. - If confused, open the Frama-C gui with
f8.
Note: There is a 10 second time limit on the proof search.
Every source block is in ‘focus’ when the variables NAME and NAMECode refer to it.
Details
(setq Language "c" LanguageExtension "c") (setq NAMEEXT (buffer-name) NAME (file-name-sans-extension NAMEEXT)) (setq NAMECode (concat NAME "." LanguageExtension))
We explicitly change focus using [not-]currently-working-with methods.
Details
(defun buffer-name-sans-extension () "" (file-name-sans-extension (buffer-name)) ) (defun currently-working-with (&optional name) "Provide the name (without extension) of the source block's resulting file. The name is then tied to the “NAMECode” global variable utilised by the “show-code” method, <f7>, and the “interpret” command's global variable “NAME”. If no argument is provided, we use “⟪BufferName⟫.c” as default file name. " (unless name (setq name (buffer-name-sans-extension))) (setq NAME name) (setq NAMECode (concat name ".c")) ) (defun not-currently-working-with (&optional name) "When “:tangle fn” has “fn” being the empty string, the tangle does not transpire. As such, it is as if we are not actually generating the source block. This operation only returns the empty string and does not alter any existing state. If we alter state, then earlier invocations to (currently-working-with) are rendered useless! " "" ;; Our return value. )
Notice that the InteractiveWayToC.el methods –<F6> to <F9>– target the
source block(s) with (currently-working-with name) where name is the most
recent name. Note that the name component need not be unique: Blocks having
the same one write to the same file.
In a new line enter <s then at the end press TAB to obtain a nice hello-world
template. Some code will be generated for you –free of charge–, edit it as you like.
Details
(make-variable-buffer-local 'org-structure-template-alist) (setq TEMPLATE (concat "#+NAME: ???? -- goal of this code block" "\n#+BEGIN_SRC " Language " :tangle (currently-working-with \"HelloWorld\") \n" "#include<stdio.h> // for IO" "\nint main() \n{\n printf(\"--Hello, World!--\");\n return 0; \n}" "\n#+END_SRC")) (add-to-list 'org-structure-template-alist `("s" ,TEMPLATE))
Then to see the code generated by this file press M-x then enter show-code then enter;
alternatively, press C-x C-e after the final parenthesis: (show-code).
My definition of (show-code) begins with closing the code buffer if it exists,
then continue by extracting the most recent code and displaying it below the current buffer.
The definition of (interpret) is nearly the same except we switch to an output buffer,
and create it if it doesn't exist.
Note that our interpretation command is essentially the following command line invocation:
NAME=myfilename ; gcc $NAME.c -o $NAME.exe ; ./$NAME.exe
Details
(defun show-code () "Show focused source blocks in a new buffer." (interactive) (ignore-errors (kill-buffer NAMECode)) (save-buffer) (org-babel-tangle) (split-window-below) (find-file NAMECode) (other-window 1)) ;; Since there are many generated files, let's mention the name ;; of the program file currently being executed, or proven. ;; (defun insert-focused-name () "Insert the name of the focused source blocks at the beginning of the buffer." (beginning-of-buffer) (insert "================\n⟪ " NAME ".c ⟫\n================\n\n")) (defun interpret () "Execute focused source blocks in a new buffer." (interactive) (save-buffer) (org-babel-tangle) (switch-to-buffer-other-window "*Shell Command Output*") (shell-command (concat "cd " default-directory "; NAME=" NAME " ; gcc $NAME.c -o $NAME.exe ; ./$NAME.exe")) (insert-focused-name) ;; Go back to the literate buffer. (other-window 1)) (defun frama-c () "" (interactive) (save-buffer) (org-babel-tangle) (shell-command (concat "frama-c-gui " NAMECode " -wp -rte &"))) (defun try (this that) "" (condition-case nil (eval this) (error (eval that))))
The frama-c-no-gui command tries to find where an error happens by placing the cursor
near an unproven assertion. It does so by looking for the phrase false in the shell output
buffer after the frama-c program is invoked. If it cannot find it, you are placed at
the end of the buffer and, ideally but not necessarily, should see all goals have passed.
Details
(defun frama-c-no-gui () "" (interactive) (org-babel-tangle) ;; Avoid generating proof goal statements --for now. ;; (shell-command (concat "frama-c " NAMECode " -wp -wp-msg-key=print-generated -rte")) (shell-command (concat "frama-c " NAMECode " -wp -wp-timeout 10 -rte")) (switch-to-buffer-other-window "*Shell Command Output*") (insert-focused-name) (hl-line-mode) (setq frama-c-state (catch 'state ;; Global variable indicating current state (dolist (elem '("Exercise" "unknown" "user error" "false" "Timeout" "Proved goals")) (beginning-of-buffer) (try '(and (search-forward elem) (throw 'state elem)) 'nil) ))) ;; global variable about status (setq frama-c-status (format "Frama-C: %d﹪ of proof complete!" (frama-c-progress))) ;; Use the red colour of failure. (set-face-background 'hl-line "pink") ;; Or did we succeed? ;; We might have halted a “false” *constant* even though all goals pass. ;; ⟨ This is not an issue when proofs are not being generated. ⟩ (if (equal frama-c-state "Exercise") (setq frama-c-status (concat frama-c-status " ⟪There are holes!⟫")) (when (or (equal frama-c-state "Proved goals") (eq (frama-c-progress) 100)) (set-face-background 'hl-line "pale green") (try '(search-forward "Proved goals") t))) (message frama-c-status) (minimize-window) ;; Make current buffer roughly 3 lines in height. )
Where the frama-c-progress command yields the percentage denoting the number of goals proven.
Details
(defun frama-c-progress () "" (let ( (here (point)) ) (beginning-of-buffer) (try '(search-forward "Proved goals:") 0) ;; (kill-line) (copy-region-as-kill (point) (point-at-eol)) (goto-char here) (* 100 (string-to-number (calc-eval (current-kill 0)))) ))
Finally,
Details
(local-set-key (kbd "<f6>") 'interpret) (local-set-key (kbd "<f7>") 'show-code) (local-set-key (kbd "<f8>") 'frama-c) (local-set-key (kbd "<f9>") 'frama-c-no-gui)
It is to be noted: I only know enough Elisp to get by.
Again: Hope you had fun!



